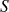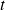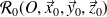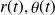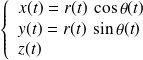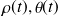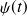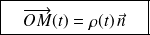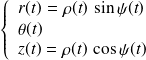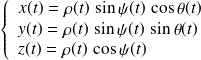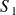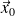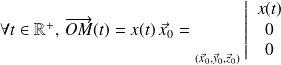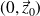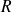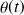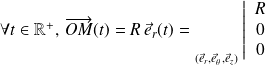C03_P1 : Cinématique du solide

Afficher le planAfficher le plan

Position d'un point d'un solide dans un référentiel

Définition

La position d'un point lié à un solide , à un instant , dans le repère de référence est définie à l'aide d'un vecteur appelé vecteur position :

Coordonnées cartésiennes
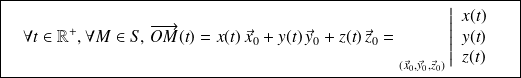
\boxed{ \quad \forall t \in \mathbb{R}^+, \forall M \in S, \, \overrightarrow{OM}(t)= x(t) \, \vec x_0 + y(t) \, \vec y_0 + z(t) \, \vec z_0 = {\vphantom{\left\{\begin{array}{ccc}a\\b\\c\\\end{array}\right\}}}_{(\vec x_0, \vec y_0, \vec z_0)}{ } \left | \begin{array}{c}x(t) \\y(t) \\z(t) \end{array} \right . \quad }

On utilise trois paramètres pour définir complètement la position du point 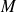dans le repère de référence. Ceux-ci dépendent du système de coordonnées dans lequel est exprimé le vecteur position.

Dans le cas ci-dessus, le vecteur position est exprimé dans un système de coordonnées cartésiennes. les trois paramètres de position son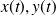t : et .

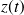On utilise aussi couramment les systèmes de coordonnées cylindriques et sphériques :

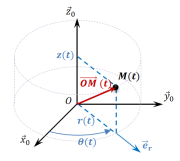  • Coordonnées cylindriques :

Paramètres du mouvement : et

Correspondance avec les coordonnées cartésiennes :

Coordonnées cylindriques

  • Coordonnées sphériques :

Paramètres du mouvement : et

Correspondance avec les coordonnées cylindriques :

Correspondance avec les coordonnées cartésiennes :

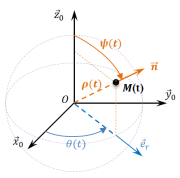Coordonnées sphériques

Paramétrage d'un mouvement de translation rectiligne

Dans le cas de la translation rectiligne, un seul paramètre géométrique linéaire (variable) est nécessaire pour définir la position d'un solide à tout instant.

Exemple

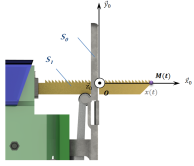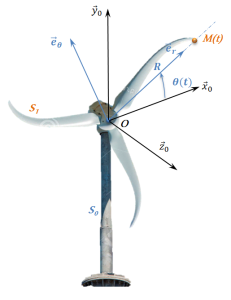
Soit , un point d'un un solide en translation rectiligne de direction par rapport au repère de référence . Dans ce cas, x(t) est le seul paramètre nécessaire pour connaître la position du solide   à tout instant :

Paramétrage d'un mouvement de rotation autour d'un axe fixe

Lorsqu'un solide a un mouvement de rotation, un seul paramètre géométrique angulaire est nécessaire pour définir sa position à tout instant.

Exemple

Soit , un point d'un un solide en rotation autour de l'axe fixe par rapport à au repère de référence . La distance de ce point à l'axe, ou rayon , reste constante au cours du mouvement.

Dans ce cas, est le seul paramètre nécessaire à la définition de la position du solide  :

Remarque

La paramètre 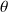n’apparaît pas explicitement dans l'expression du vecteur position. Celui-ci est présent à travers le vecteur 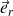, dont l'orientation dépend directement de cet angle.

En fait 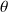positionne la base cylindrique 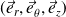en rotation par rapport à la base cartésienne .

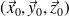On peut alors chercher à exprimer le vecteur position dans la base cartésienne en fonction du paramètre 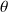. Cela fait appel aux notions de changement de base.

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimerRéalisé avec Scenari (nouvelle fenêtre)